Чтобы рассчитать осадку фундамента и проверить прочность (несущую способность) основания, нужно знать распределение напряжений в основании, т. е. его напряженное состояние. Необходимо иметь сведения о распределении напряжений не только по подошве фундамента, но и ниже нее, так как осадка фундамента является следствием деформации толщи грунта, расположенной под ним. Для расчета несущей способности основания также приходится определять напряжения в грунте ниже подошвы фундамента. Без этого нельзя установить наличие и размеры областей сдвигов, проверить прочность прослойки слабого грунта и т. д.
Для теоретического определения напряжений в основании используют, как правило, решения теории упругости, полученные для линейно деформируемого однородного тела. В действительности грунт не является ни линейно деформируемым, телом, так как деформации его не прямо пропорциональны давлению, ни однородным телом, так как плотность его меняется с глубиной. Однако эти два обстоятельства не сказываются существенно на распределении напряжений в основании.
В данной главе рассматриваются не все вопросы напряженного состояния оснований, а только методика определения нормальных напряжений, действующих в грунте по горизонтальным площадкам.
Распределение напряжений по подошве фундамента
В мостовом и гидротехническом строительстве, как правило, применяют жесткие фундаменты, деформациями которых можно пренебречь, поскольку они малы по сравнению с перемещениями, связанными с осадкой.
Измерения нормальных напряжений (давлений) по подошве фундамента, выполненные с помощью специальных приборов, вмонтированных на уровне подошвы, показали, что эти напряжения распределены по криволинейному закону, зависящему от формы и размеров фундамента в плане, свойств грунта, среднего давления на основание и других факторов.
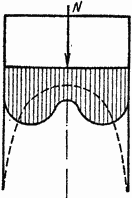
В качестве примера на рис. 2.1 сплошной линией показано фактическое распределение нормальных напряжений (эпюра нормальных напряжений) по подошве фундамента, когда нагрузка (сила N) значительно меньше несущей способности основания, а пунктиром — распределение напряжений, полученное на основе решений теории упругости.
В настоящее время, несмотря на накопленный экспериментальный материал и теоретические исследования, не представляется возможным устанавливать в каждом конкретном случае действительное распределение давлений по подошве фундамента. В связи с этим в практических расчетах исходят из прямолинейных эпюр давлений.
Рис. 2.2. Прямолинейные эпюры нормальных напряжений по подошве фундамента а — при центральном сжатии; б— при внецентренном сжатии и e< W/A; в — при внецентренном сжатии и е> W/AПри центральном сжатии (рис. 2.2, а) напряжения Pm, кПа, по подошве принимают равномерно распределенными и равными:
Pm = N/A, (2.1)
где N — нормальная сила в сечении по подошве фундамента, кН; А — площадь подошвы фундамента, м2.
При внецентренном сжатии эпюру напряжений принимают в виде трапеции (рис. 2.2, б) или треугольника (рис. 2.2, в). В первом из этих случаев наибольшее ртах и наименьшее Pmin напряжения определяются выражениями:
Pmax = N/A + M/W;
Pmin = N/A – M/W (2.2)
где M — Ne — изгибающий момент в сечении по подошве фундамента, кН·м (здесь е — эксцентриситет приложения силы N, м); W — момент сопротивления площади подошвы фундамента, м3.
Формулы (2.2) справедливы в случаях, когда изгибающий момент действует в вертикальной плоскости, проходящей через главную центральную ось инерции подошвы фундамента.
При подошве фундамента в виде прямоугольника с размером, перпендикулярным плоскости действия момента М, b и другим размером a имеем A = ab и W = ba2/6. Подставляя выражения A и W в формулы (2.2) и учитывая, что M = Ne, получаем:
Pmax =N/ba(1+6e/a)
Pmin=N/ba(1-6e/a) (2.3)
Напряжение Pmin, кПа, вычисленное по формуле (2.2) или (2.3) при эксцентриситете e> W/A, получается отрицательным (растягивающим). Между тем в сечении по подошве фундамента таких напряжений практически быть не может. При е> W/A край подошвы фундамента, более удаленный от силы N, поднимается под действием этой силы над грунтом. На некотором участке подошвы фундамента (со стороны этого края) контакт между фундаментом и грунтом нарушается (происходит так называемое отлипание фундамента от грунта), а потому эпюра напряжений P имеет вид треугольника (см. рис. 2.2, в). Этого обстоятельства формулы (2.2) и (2.3) не учитывают, поэтому ими нельзя пользоваться при е> W/A.
Формулы для определения размера а1, м, части подошвы, по которой сохраняется контакт фундамента с грунтом, и наибольшего напряжения Pmax, кПа (см. рис. 2.2, в), можно получить, если учесть, что напряжения P должны уравновесить силу N, кН, действующую на расстоянии с от ближайшего к этой силе края подошвы фундамента.
Отсюда вытекают два условия: 1) центр тяжести эпюры напряжений P расположен на линии действия силы N; 2) объем эпюры равен величине этой силы. Из первого условия при прямоугольной подошве фундамента следует
А1=3с, (2.4)
а из второго
(Pmax а1/2)b = N. (2.5)
Из формул (2.4) и (2.5) получаем
Pmax =2N/(3cb). (2.6)
Итак, при эксцентриситете е> W/A = a/6 наибольшее давление по прямоугольной подошве фундамента Pmax следует определять по формуле (2.6).