Парке́т — мощение плоскости многоугольниками без пробелов и перекрытий, в котором любые два многоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек.
Математики из Вашингтонского университета в Ботелле открыли новый тип пятиугольных паркетов —выпуклых пятиугольников, которыми можно настелить плоскость без пробелов и наложений. Ранее было известно только 14 типов таких пятиугольников, последний из которых был открыт 30 лет назад. Об этом сообщает издание The Guardian.
Нет, на фото это конечно не он. Вот про него подробее …
Проблема нахождения и классификации паркетных многоугольников является одной из наиболее актуальных в современной комбинаторной геометрии. Известно, что любым треугольником и четырехугольником можно настелить плоскость, а также то, что существуют только три типа выпуклых шестиугольников, способных выполнить такую же задачу.
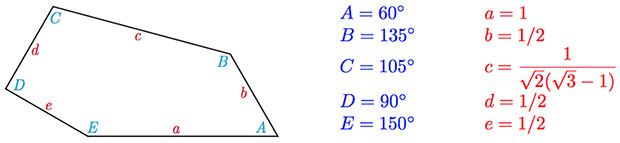
Фигурами, которые имеют более шести сторон, настелитьт плоскость невозможно.До сих пор математикам не известно точное число типов пятиугольников, способных замостить плоскость.
Первую классификацию таких пятиугольников осуществил в 1918 году математик Карен Рейнхард, описавший пять типов фигур. В период с 1968 по 1985 год четырьмя другими учеными были найдены еще девять типов аналогичных многоугольников. Открытие американскими учеными 15-го типа пятиугольников стало первым за последние 30 лет.
Проблема классификации выпуклых пятиугольников, которыми можно замостить плоскость, является красивой и достаточно простой математической задачей, доступной для понимания даже детям. Эта проблема уже в течение ста лет не имеет полного решения. Связь этой задачи с 18-й проблемой Гильберта.
Учные отметили, что пока не знают, найдут ли новые типы пятиугольников, которые могут замостить плоскость. С этой целью математики собираются продолжить свои исследования, представляющие собой перебор на компьютере существующих возможностей.
Известно что исследование пятиугольных фигур представляет не только академический, но и практический интерес. «Многие структуры, которые мы видим в природе, например капсиды вирусов, состоят из специальным образом формирующих свою геометрию и динамику строительных блоков, объединяющихся вместе для формирования структуры большего масштаба», — говорит математик.

